GEOL2301: Palaeoecosystems

We're going to learn how to interpret life history from assemblage data.

You can choose between using a point-and-click interface within R (straightforward) or constructing the plots yourself, by hand, spreadsheet, or writing your own code (which will help you obtain a deeper understanding of the methods.)

Thayer (1977) report length measurements (in mm) from 42 terebratulid brachiopods that died between censuses conducted in 1974 and 1975.

Getting the data

Save the data file to your computer, and inspect its contents.

• To save a file from the internet, right-click the link and select "Save file as…" (Windows) or "Download linked file as…" (Mac). Save the file somewhere you'll be able to locate it later.

The format is simply a list of measurements, separated by spaces.

Open the histogram plotter

• In the RStudio console, type palec::Histogram() to run the histogram 'app'.
  • You can resize the viewer, or click the icon to launch the app in a separate web browser, to gain a little more space.
• Click 'Browse…' to load the data you saved to disk. The histogram will update automatically, showing the frequency of taxa with different lengths.
• Set the X Label to "length / mm".

Save your plot in a convenient format using one of the download buttons, then answer the questions below. Write your answers down before clicking on them for my answers.

• Do the data fit a normal distribution, or are they right-skewed (longer tail on the right) or left-skewed?
• Use the “Fit Normal” checkbox to overlay the normal distribution that best matches the data.
• Adjusting the bin size (number of bins) sometimes gives a clearer perspective.

• Would you agree that the 'hump' of the distribution is slightly to the right of the mean (i.e. the centre of the reference normal distribution)? This would denote a slight left skew, consistent with the slightly negative skewness value (−0.2153).

  Skewness values smaller than ±0.5 are typically considered to be negligible, so you would be justified in treating terebratulid length as normally distrubtued.

• What does the skewness suggest about the level of infant mortality?
• If infant mortality were high, then most dead brachiopods would be little, so we'd expect the peak of the distribution to be on the left of the mean (i.e. positive skew).

Open the survivorship plotter

• In the RStudio console, press Esc to terminate the Histogram app, then launch the survivorship app by running palec::Survivorship().
• Load the terebratulid data again. The survivorship plot will update automatically, showing the proportion of individuals that survived to each age (i.e. size).
• Configure the plot as necessary.
  • Which axes should be log-transformed?
  • If size is a linear approximation of age, then the x axis should be linear. As survivorship represents the rate of death at any given age, the y axis should be log transformed.

• Is this survivorship curve:
• Type I (convex)
• Type II (linear)
• Type III (concave)
• Type I: most juveniles survive to adulthood.

Careful examination of the living terebratulids determined that older individuals grow more slowly. The age of an individual thus scales with log(length).

Log-transform the x-axis, so that it represents a better proxy for age (rather than size).

• Does this affect your interpretation?
• Our previous interpretation is now reinforced. In this case, the transformed data give a more “honest” picture, as our x-axis now corresponds more closely to age, which is what we ideally want to plot – size is just a proxy.

Bringing it together

Now let's combine these insights to consider the likely life history of these terebratulids.

• Based on the information from the size-frequency analysis and the survivorship plot, are the terebratulids more likely to be:
• r-selected
• K-selected
• K-selected: low infant mortality implies high resource investment in a small number of offspring.

• Are they likely to be associated with:
• Early successional communities
• Climax communities
• K-selected taxa tend to be specialist competitors, well suited to mature climax communities.

• As such, would you expect the taxon’s original community to be:
• High diversity
• Low diversity
• Climax communities tend to have had time to reach a reasonably high species richness, with low dominance.

Extension exercise

If you've got time, use a text editor such as Notepad++ to create your own .txt documents and load them into the plotters. Can you create a dataset that corresponds to each of the three survivorship curve trajectories? Does the skew of these datasets correspond to what you expect?

Now we're going to look at assemblage-level data in order to explore changes in the successional stage of an entire community.

Our data (download) are species counts from ten 5–10 kg samples taken at intervals from an Ordovician sedimentary succession in Wales (from Williams et al. 1981; see graphical log).

Launch the palec::Diversity() app and load the Llanvirn.txt data. Cross-reference the species with those shown below.

Each column in the input dataset represents a different assemblage. Start by selecting assemblage CD6.

• What are your initial impressions of the diversity and dominance of this assemblage? Which taxon/taxa would you expect to form the trophic nucleus?

• Fair diversity (richness & evenness), slightly dominated by the trilobite Basilicus and the brachiopod Sowerbyella.

Next, we'll compare CD6 with the underlying and overlying assemblages, CD5 and CD7. Note from the log that these represent quite different environments, separated by unconformities. Look at the bar plots to get a feel for the relative species richness and dominance of assemblages CD5–CD7.

• Note the different x axis scales, denoting different sample sizes. Use the "Axis size" slider to compare the assemblages to the same scale.
• Looking for now just at the bar plots, mark each of these three communities on the crude spectra below.
• As an example, I've sketched in assemblage CD1, which has very low species richness and is strongly dominated.

• There's no right answer here, as it's a subjective exercise, but here are observations that may have guided your hand:

  CD5 is super-dominated by one species, even though a fair number of rare species are present.

  CD6 is quite rich, with two dominant species but a number of mid-abundance species too. When ordered by rank abundance, do the bars look like they might exhibit a geometric distribution?

  CD7 has a low richness – perhaps just because few individuals have been collected? Looks even.

• Double click the white "×" button to clear the canvas.

Now we're going to explore some of the quantitative indices of diversity, to see how they measure up against the intuitive assessment that you just made.

Look at the diversity indices for each assemblage, displayed beneath the bar plot.

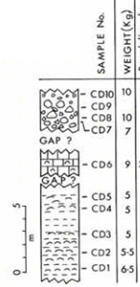
• Rank assemblages CD5–CD7 from least to most diverse, based on their Species richness (S).
• • Least diverse
  • CD7 (S = 8)
  • CD5 (S = 14)
  • CD6 (S = 15)
  • Most diverse
• Do you think that this metric is a reliable measure of diversity?
• Hint: look at the number of individuals sampled in each assemblage.
• n is tiny in CD7, and huge in CD6. Clearly, when n is very small relative to S, you are not going to sample every species that is present. It is going to take a very large sample indeed to observe the rarest species.
• Have a go at devising a formula that will allow the species richness of two assemblages, each containing a very different number of individuals, to be compared.
• Getting the "right answer" is not important here: I'm interested in your thought process.
• To backstrip the effect of sampling intensity (n) on S, you need some concept of how many more rare species you will happen to see as you sample more individuals. You can then 'shrink' S by this function of n. The next section gives two widely used approaches. Neither is "correct" – the 'right' approach for a specific situation is somewhat unknowable.

Richness indices

Menhinick’s and Margalef’s richness 'indices' are two attempts to normalize the number of species observed based on the number of individuals sampled.

The two approaches differ in their concept of how many more 'rare' species we expect to see as we sample more individuals: Menhinick's (S / √n) posits that the number of species increases with the square root of the number of individuals sampled; Margalef's ((S – 1) / ln n) that S should increase with the logarithm of sample size. Empirically, which is a better model seems to vary from assemblage to assemblage, so neither is necessarily “better”.

• How does each approach order the three assemblages?
• • Menhinick’s richness: Least diverse _6_ / _5_ / _7_ Most diverse
  • Margalef’s richness: Least diverse _5_ / _6_ / _7_ Most diverse
• Does it matter which you choose to calculate?
• It looks wise to calculate both: if different indices suggest different rankings, then perhaps it's worth pondering whether sample size is affecting your results, and not putting too much weight on rankings that disagree.
• The coloured bars beside each value contextualize the value, where a zero-width bar represents minimum richness, and a full width bar maximum richness. Notice that despite their very different absolute values, Menhinick and Margalef's measures always sit in a very similar place in their respective ranges.

Dominance indices

Now let’s consider how we might measure dominance.

It's a good idea to measure this using an index: mathematically, an index is a dimensionless value that ranges from zero to one. In this context, a value of one should denote maximum dominance; zero, maximum evenness.

The simplest measure, and the one that you are perhaps most likely to encouter, is the Berger–Parker index. The BPI is the proportion of the n individuals that belong to the most common taxon (n_t) – i.e. n_t / n.

Worked example:

Species A: 5 individuals
Species B: 15 individuals
Species C: 10 individuals
Species D: 10 individuals

n = 5 + 15 + 10 + 10 = 40 individuals

Most common taxon = Species B (15 individuals)

n_t = 15

BPI = n_t / t = 15 / 40 = 3 / 8 = 0.375

• Consider two assemblages, A and B. A has a dominance index of 0.25. B has a dominance index of 0.25. Which is more dominated?
• This is a somewhat mischevious question. Answer it anyway...
• You would expect that both assemblages would be equally dominated, and not particularly dominated at that (i.e. rather even). If that's not the case, then you might want to ask hard questions of the supposed 'index'.
• Consider an assemblage that contains 48 individuals and four species. What is the range of possible values that the Berger–Parker index can take?
• Hint: Consider two scenarios: one where an assemblage is maximally dominated, one where it is maximally even.
• • Create a file containing these two assemblages, and load them into the Diversity viewer, to check your answers.
  • Set up a spreadsheet that will calculate the BPI as you edit the number of individuals and number of species, then play with the figures to see how the BPI changes.

• Maximum is obtained when: n₁..₄ = 45, 1, 1, 1.
  n_t / n = 45/48 = 15/16 ~ 1

  Minimum is obtained when: n₁..₄ = 12, 12, 12, 12:
  n_t / n = 12/48 = 1/4 ≫ 0

• More generally, what value does the Berger–Parker index take in an assemblage of n individuals that has perfect evenness (i.e. minimum domination)?
• You may need to express this value in terms of the species richness S.
• n / S < n_t < (n − S), so
  (n / S × 1 / n) = 1 / S ≤ BPI < 1
• Do the Berger-Parker index values for each assemblage match up with your evaluation of their relative dominances? Do you intuitively agree, based on the graphs, that assemblages CD6 and CD7 have very similar dominances?
• BP{CD6} ~ BP{CD7} ~ 0.47. But BPmin{CD6} = 1/15 = 0.06; BPmin{CD7} = 1/8 = 0.125 So BP{CD6} is further from its minimum value than BP{CD7}!
• Now's a good time to revisit those two assemblages with a BPI of 0.25. What else do you need to know about the assemblages to work out which is more dominated? How useful is the BPI as a measure of dominance?

• The BPI is not an index: it does not really vary from zero to one.

  To interpret the BPI, you really need to know S, and you probably want to know n too.

  Is it just me, or does the BPI seem to complicate, rather than simplify, the interpretation of an assemblage?

• To mitigate these effects, I've added an option in the Diversity app to correct visualization of the BPI and related values for sample size effects, such that a zero-width bar corresponds to the lowest possible value, and a full-width bar corresponds to the highest.

  Use the "Correct range for sample size" tickbox to see how much difference this makes in practice – what properties characterize the most-affected assemblages?

Simpson Index

Did you notice in your calculations that the Berger–Parker index only incorporates the dominance of the most abundant taxon?

It doesn't seem right that these two assemblages would be considered equally dominated:

Species:	A	B	C	D	n
Assemblage X:	25	25	1	1	52
Assemblage Y:	25	9	9	9	52

The Simpson index of dominance addresses this concern. It is given by Σ p_i², where p_i is the proportion of individuals belonging to taxon i.

• What are the Simpson indices of these two assemblages?
• X: 0.46; Y: 0.32.
  Does this agree with your intuition as to which was more dominated?
• What range of values can this index take for an assemblage with S species?
• 1 / S ≤ D < 1 (again)

Shannon entropy / Equitability

The Shannon entropy, given by –Σp_i ln p_i, is a related but more pleasing measure of dominance.

Entropy reflects how likely you are to win a bet on what species the next individual to be sampled will belong to – in a dominated community, a bet on the dominant species will usually pay out.

Entropy is a measure of information (the average information content of an outcome), measured in non-arbitrary units (bits – the same unit of data that measures your broadband speed). As such, this is the only measure that has any objective meaning.

With some simple maths, this can be normalized to run from 0 (entirely dominated) to 1 (maximum evenness); this is reported as the Equitibility (J).

• How do these three metrics of dominance compare with one another, and with your intuition, for the three assemblages?
• J ranks 5 < 6 < 7. Does this match the ‘intuitive’ order you sketched on the diagram earlier?

Application

Time to put this theory into practice. Examine each of the ten samples in the succession. View their individual graphs, then compare their dominance and diversity.

• Can you detect any trends as time goes by (from assemblage CD-1 to assemblage CD-10)?
• CD1→5 are all low diversity and dominated by a single species. CD6→10 (except perhaps 9) are richer and less dominated.

Whittaker plots

Now we will transform our data to generate rank-abundance plots.

• In the Diversity app, select "Order by rank abundance". That's the 'rank' bit taken care of.
• We need to log-transform the abundance – handily, there's a box for that too. Make sure it's checked.
• To make the graph easier to interpret, we want to rotate it, and present it as points rather than bars. Select "Scatter plot" to accomplish this.
• You can add a 'line of best fit' with the "Fit (log)linear" option: useful for evaluating possible geometric distributions.
• Do any assemblages approximate (loosely) the straight line expected of a geometric distribution? Do others approximate the S-shape of the log-normal distribution, with few common and few rare species?
• Don’t get thrown by “steps” in the data associated with jumps from one integer count to the next. Many species may be represented by a single individual – you can’t count 1.3 brachiopods.
• Use Octave plots to validate your answers

• CD6, and perhaps CD7–9, almost look linear: but can you detect that faint S-shape? The most abundant species are certainly more dominant than predicted by a geometric model.

  Octave plots reveal a possible log-normal distribution for these assemblages; the high values of Shapiro's p (> 0.05) indicate that a log-normal distribution cannot be rejected.

  Many others assemblages, e.g. CD2–3, have one or two superabundant species far above the line – perhaps representing ‘pioneers’? Could these counts represent an artefact of some sort? Would this affect the bigger picture?

Synthesis

Now it’s time to bring all these observations together.

• From what you know about the ecology of the constituent organisms, reconstruct the palaeoenvironment in which they dwelt and provide a geological and ecological interpretation for any variation in diversity and dominance, and the shape of rank abundance plots, through the sedimentary sequence.
• You may wish to refer to Fossils at a Glance and Scott's reference ternary plots.
• • Mostly suspension feeders: high energy, ?below photic zone.
  • Steady increase in richness & evenness through time, with later assemblages exhibiting log-normal distributions: does this reflect more stable environments, or removal of stressors? Why so many trilobites in CD6?
• Are your interpretations consistent with the sedimentary log?

• Lower log shows stable, ?low resource, ?low oxygen = stressful settings. Low energy suggests that detritovores might dominate. Might occasional anoxia stop ecosystems maturing to climax communities?

  Over time, energy levels increase (decrease in water depth?). Suspension feeding becomes preferable? Shallower water → photic zone; more food → more predators → more diversity? Climax communities becoming established, with log-normal distribution.

  Does CD6 (unconformity-bounded limestone) have a unique character?